CSP-J初赛模拟卷2
由四个没有区别的点构成的简单无向连通图的个数是( )。
6
7
8
9
下面的故事与( )算法有着异曲同工之妙。 从前有座山,山里有座庙,庙里有个老和尚在给小和尚讲故事:“从前有座山,山里有座庙,庙里有个老和尚 在给小和尚讲故事:‘从前有座山,山里有座庙,庙里有个老和尚给小和尚讲故事……’”
枚举
递归
贪心
分治
以下排序算法中,不需要进行关键字比较操作的算法是( )。
基数排序
冒泡排序
堆排序
直接插入排序
如果开始时计算机处于小写输入状态,现在有一只小老鼠反复按照CapsLock、字母键A、字母键S 和字母键 D 的顺序循环按键,即CapsLock、A、S、D、CapsLock、A、S、
A S D a
有 10 个顶点的⽆向图⾄少应该有( )条边才能确保是⼀个连通图
9
10
11
12
5 个⼩朋友并排站成⼀列,其中有两个⼩朋友是双胞胎,如果要求这两个双胞胎必须相邻,则有( )种不同排列⽅ 法
48
32
24
72
10 个三好学⽣名额分配到 7 个班级,每个班级⾄少有⼀个名额,⼀共有( )种不同的分配⽅案。
84
72
56
504
若有如下程序段,其中s、a、b、c均已定义为整型变量,且a、c均已赋值(c大于0)

s = a - c;
s = a - b;
s = s - c;
s = b - c;
把8个同样的球放在5个同样的袋子里,允许有的袋子空着不放,问共有多少种不同的分法?() 提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算同一种分法。
22
24
18
20
一棵二叉树如右图所示,若采用顺序存储结构,即用一维数组元素存储该二叉树中的结点(根结点的下标为 1,若某结点的下标为i ,则其左孩子位于下标2i处、右孩子位于下标2i+l处),则该数组的最大下标至少为 ()。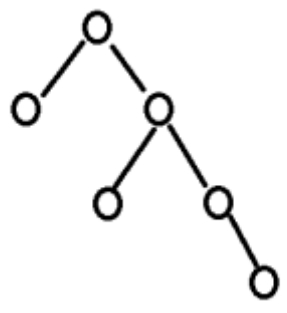
6
10
15
12
319和377的最大公约数是()。
27
33
29
31
新学期开学了,小胖想减肥,健身教练给小胖制定了两个训练方案。 方案一:每次连续跑3公里可以消耗300千卡(耗时半小时); 方案二:每次连续跑5公里可以消耗600千卡(耗时1小时)。 小胖每周周一到周四能抽出半小时跑步,周五到周日能抽出一小时跑步。 另外,教练建议小胖每周最多跑21公里,否则会损伤膝盖。 请问如果小胖想严格执行教练的训练方案,并且不想损伤膝盖,每周最多通过跑步消耗多少千卡?()
3000
2500
2400
2520
假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF,则其前序遍历序列为()。 A. ABCDEFGHIJ B. ABDEGHJCFI C. ABDEGJHCFI D. ABDEGHJFIC
ABCDEFGHIJ
ABDEGHJCFI
ABDEGJHCFI
ABDEGHJFIC
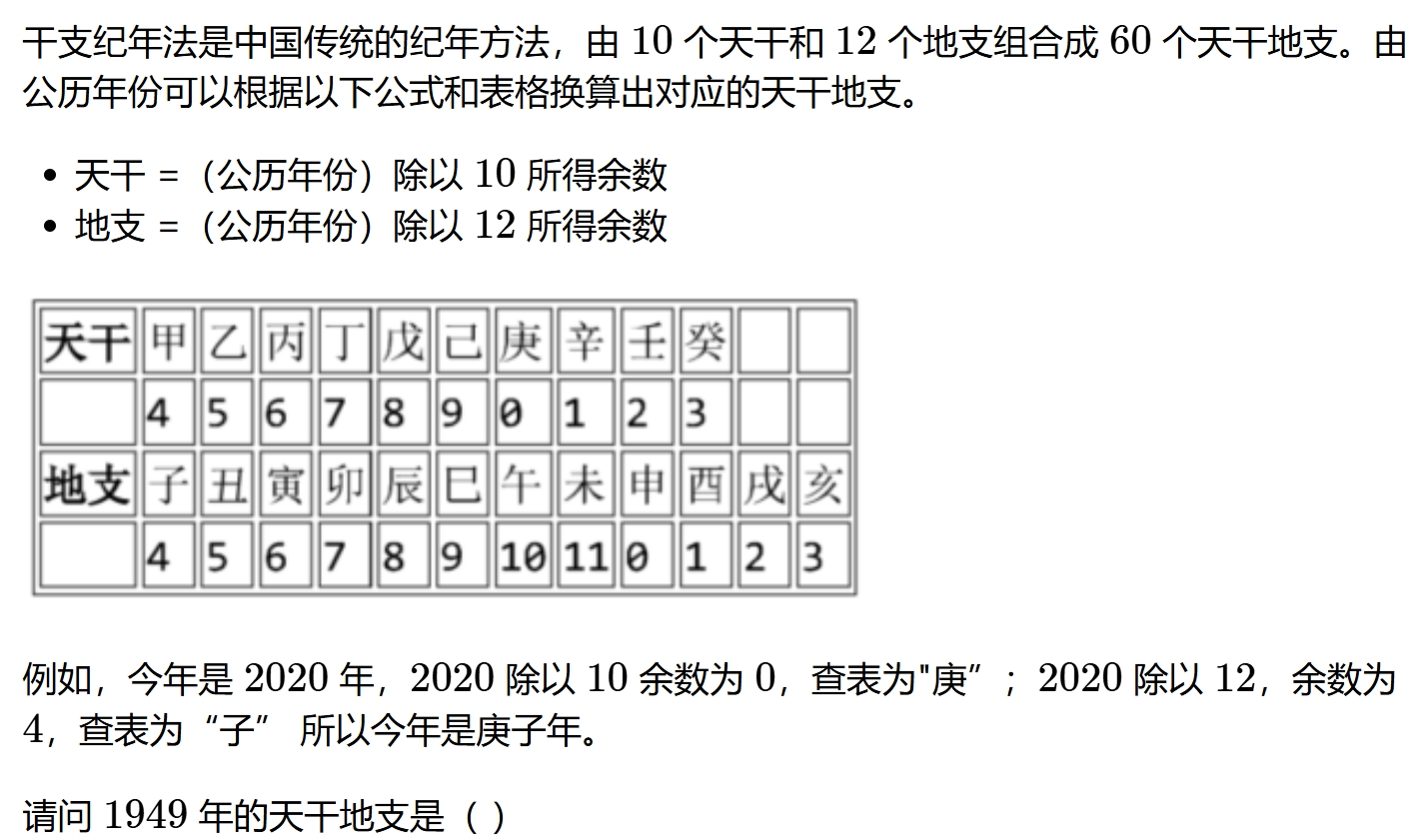
己酉
己亥
己丑
己卯
10 个三好学生名额分配到
84 72 104 44
第1题 判断
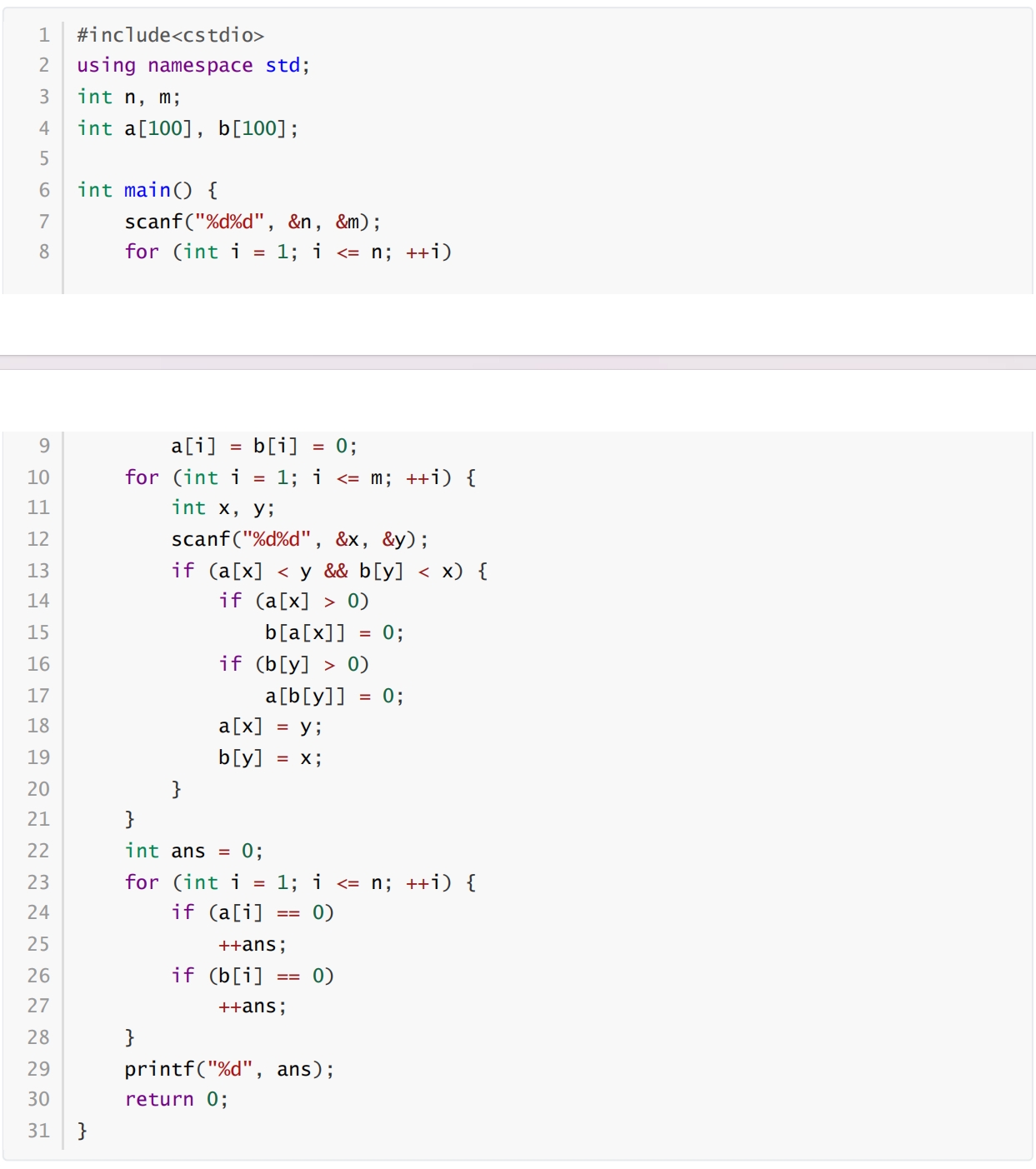
假设输入的n和m都是正整数,x和y都是在[1, n]的范围内的整数,完成下面的判断题和单选题:
•判断题
1. 当m>0时,输出的值一定小于2n。()
第2题 判断
2. 执行完第27行的 ++ans 时,ans —定是偶数。()
第3题 判断
3. a[i]和b[i]不可能同时大于0。()
第4题 判断
4. 右程序执行到第13行时,x总是小于y,那么第15行不会被执行。()
第5题 单选
•选择题 5. 若m个x两两不同,且m个y两两不同,则输出的值为()
2n-2m
2n+2
2n-2
2n
第6题 单选
若m个x两两不同,且m个y都相等,则输出的值为()
2n-2
2n
2m
2n-2m

第1题 判断
•判断题 1. 如果a数组有重复的数字,则程序运行时会发生错误。
第2题 判断
2. 如果b数组全为0,则输出为0。
第3题 单选
•选择题 3. 当n=100时,最坏情况下,与第12行的比较运算执行的次数最接近的是:
5000
600
6
100
第4题 单选
4. 当n=100时,最好情况下,与第12行的比较运算执行的次数最接近的是:
100
6
5000
600
第5题 单选
5. 当n=10时,若b数组满足,对任意0<=i<n,都有b[i] = i + 1,那么输出最大为
386
383
384
385
第6题 单选
6.(4分)当n=100时,若b数组满足,对任意0 <= i < n,都有b[i]=1,那么输出最小为.
582
580
579
581
(1)(Josephus 问题)有 ? 个人围成一个圈,依次标号 0 至 ? − 1。从 0 号开 始,依次 0, 1, 0, 1, … 交替报数,报到 1 的人会离开,直至圈中只剩下一个人。求最后 剩下人的编号。 试补全模拟程序。

第1题 单选
①处应填( )
i < n
c < n
i < n - 1
c < n - 1
第2题 单选
②处应填( )
i % 2 == 0
i % 2 == 1
p
!p
第3题 单选
③处应填( )
i++
i = (i + 1) % n
c++
p ^= 1
第4题 单选
④处应填( )
i++
i = (i + 1) % n
c++
p ^= 1
第5题 单选
⑤处应填( )
i++
i = (i + 1) % n
C++
p ^= 1

第1题 单选
三、完善程序(单选题,每小题3分,共计 3 分)
(1)(寻找被移除的元素)问题:原有长度为 n+1,公差为1等差升序数列,将数列输到程序的数组时移除了一个元素,导致长度为 n 的升序数组可能不再连续,除非被移除的是第一个或最后之一个元素。需要在数组不连续时,找出被移除的元素。
试补全程序。
①处应填( )
1
nums[0]
right
left
第2题 单选
②处应填( )
left = mid+1
right = mid-1
right = mid
left = mid
第3题 单选
③处应填( )
left = mid+1
right = mid-1
right = mid
left = mid
第4题 单选
④处应填( )
left + nums[0]
right + nums[0]
mid + nums[0]
right + 1
第5题 单选
⑤处应填( )
nums[0] + n
nums[0] + n - 1
nums[0] + n + 1
nums[n-1]
第1题 单选
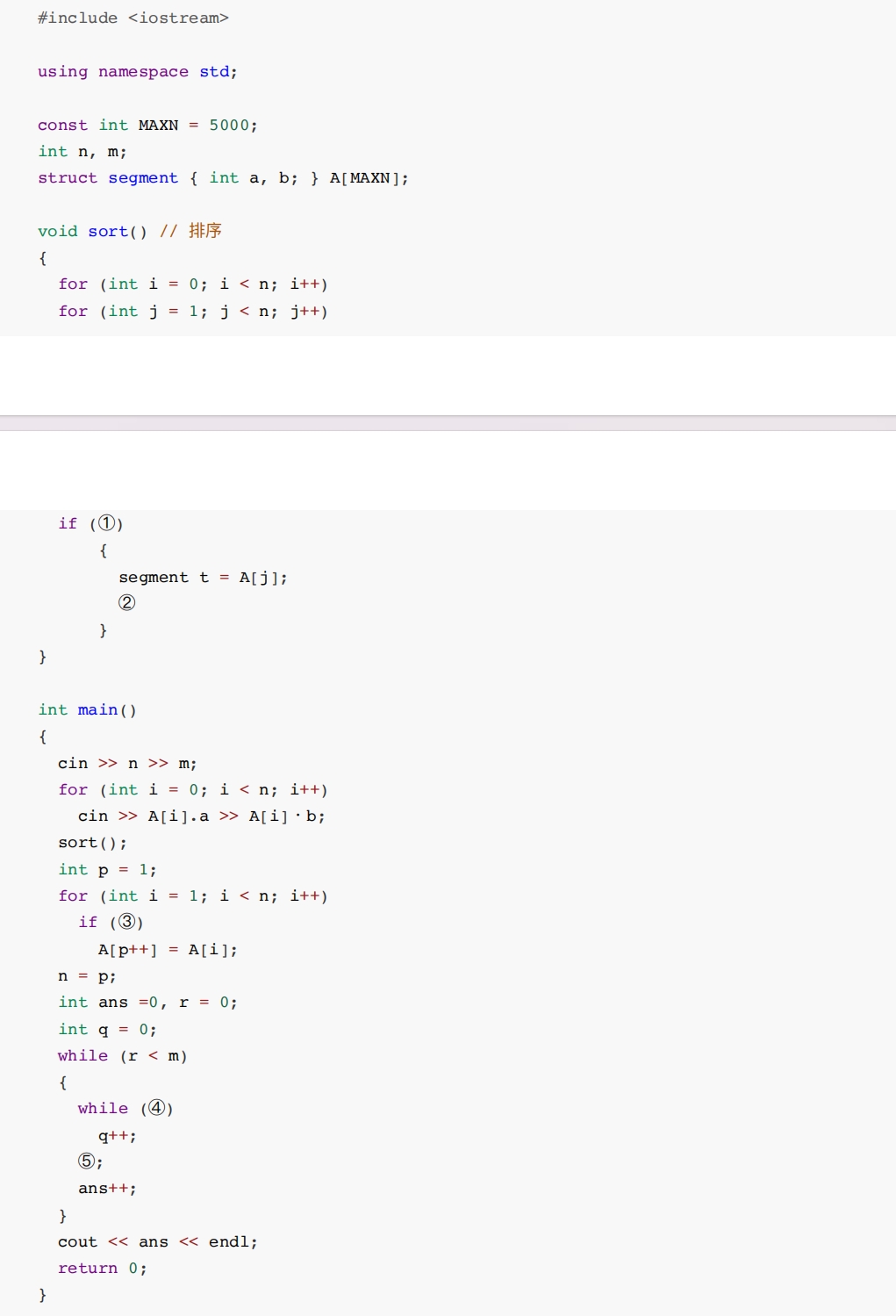
(最⼩区间覆盖)给出 n 个区间,第 i 个区间的左右端点是 [ai ,bi ]。现在要在这些区间中选出若⼲个,使得区间 [0, m] 被所选区间的并覆盖(即每⼀个 0≤i≤m 都在某个所选的区间中)。保证答案存在,求所选区间个数的最⼩值。 输⼊第⼀⾏包含两个整数
A[j].b > A[j-1].b A[j].a < A[j-1].a A[j].a > A[j-1].a A[j].b < A[j-1].b
第2题 单选
②处应填( )
A[j+1] = A[j]; A[j] = t;
A[j-1] = A[j]; A[j] = t;
A[j] = A[j+1]; A[j+1] = t;
A[j] = A[j-1]; A[j-1] = t;
第3题 单选
③处应填( )
A[i].b > A[p-1].b
A[i].b < A[i-1].b
A[i].b > A[i-1].b
A[i].b < A[p-1].b
第4题 单选
④处应填( )
q+1< n && A[q+1].a <= r
q+1< n && A[q+1].b <= r
q < n && A[q].a <= r
q < n && A[q].b <= r
第5题 单选
⑤处应填( )
r = max(r, A[q+1].b)
r = max(r, A[q].b)
r = max(r, A[q+1].a)
q++